Wave Function (Quantum Mechanics)

A wave function is a mathematical function which represents the matter-wave of a particle. It has no physical form like water waves, sound waves, or waves in springs. But we can represent or interpret it graphically. It contains all the necessary information about the particle. The interesting part is the whole Quantum Mechanics stands upon it.

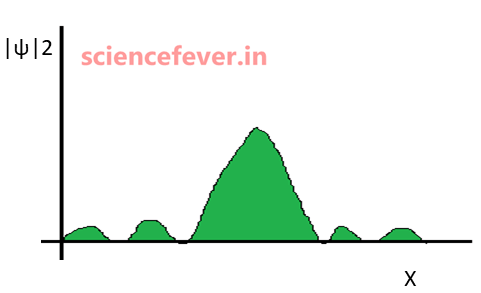
*|ψ|² gives probability density.

e.g consider an oscillator;

The equation for this system will be,\\m\frac { { d }^{ 2 }x }{ d{ t }^{ 2 } } =-kx\\

If we solve the above equation;\\x=A\cos { (\omega t+\phi ) }

If we derivate the function w.r.t. time we will get the velocity, similarly acceleration and so on. Similarly, if we operate the specific operators on the wave function(ψ) it will give specific information about the particle.

e.g. operating Hamiltonian(\frac { { -ℏ }^{ 2 } }{ 2m } { \nabla }^{ 2 }+V) gives the total energy.

It is not true that wave function can only be written as ψ. It is a mathematical function. You can write X, Y, Z, or anything in place of ψ.

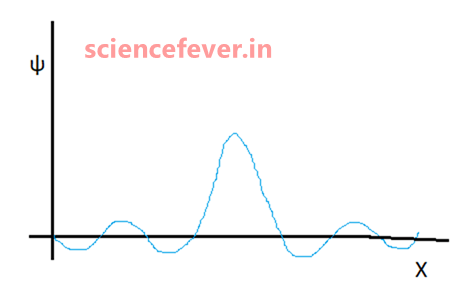
But representing a wave function as ψ makes it clear that we are dealing with quantum mechanics, quantum particle, or specifically with wave function as it is well established.

Every subject branch has its own terminology and symbols. so it will be a great way to express wave function as (ψ) except X, Y, Z or anything.

Where did the concept of wave function come from?

In 1924 Louis Broglie hypothesized that matter has dual characters i.e wave-like and particle-like. He suggested that a matter of mass m, moving with velocity v is associated with a wave of wavelength ;

                               λ = h/mv

               where λ – planks constant

Later in 1927 Davisson Germer and in 1928 Thomson experimentally showed that the theoretical prediction of the wavelength of an electron (de-Broglie wavelength) almost coincided with the experimental value.

After that Erwin Schrödinger proposed that the matter waves are represented by the wave function and using this concept he developed a second order differential equation.

FAQs:-

1.How to get a wave function?

To derive the wave function for a particular system we have to solve the Schrodinger’s second order differential equation applying the required conditions.

for example;

Consider a system where the particle encounters infinite potential beyond x=0 and x=1.

V(x)=\infty ,where\quad 0>x>a\\ V(x)=0,where\quad 0\le x\le a\\

\frac { { d }^{ 2 }\Psi (x) }{ { dx }^{ 2 } } +\frac { 2m }{{ ℏ }^ {2}}(E-V)\Psi (x)=0\\ \\ But\quad V(x)=0,0<x<a

\Rightarrow \frac { { d }^{ 2 }\Psi (x) }{ { dx }^{ 2 } } +\frac { 2mE }{ ℏ } \Psi (x)=0

\Rightarrow \frac { { d }^{ 2 }\Psi (x) }{ { dx }^{ 2 } } +{ k }^{ 2 }\Psi (x)=0

so\quad the\quad solutons\quad are;\\ { \Psi (x) }_{ 1 }=A\sin { (kx) } \\ { \Psi (x) }_{ 2 }=A\cos { (kx) }

general\quad solution\quad will\quad be;\\ { \Psi (x) }=A\sin { (kx) } +A\cos { (kx) }

2.Why |ψ|² gives probability density?

This is quite confusing. First Max Born stated that ψ gives the probability density. But later he modified it to |ψ|².

It may be because we deal with complex numbers in the case of the wave function. So to be satisfied for both the imaginary and real number he may have concluded this.

3.Why we take { e }^{ iax } but not { e }^{ ax } in case of waves?

Exponential functions (e^ax)always increase or decrease but not oscillate . But e^iax oscillates in two dimensions. So it can represent a wave. That is why we represent a wave in exponential form with addition of “i” to its power.

4.Is ψ =sinx a wave function?

A wave function must be square integrable. That means it you should disappear at infinity. But ψ =sinx does not disappear at infinity. But if you cut the x axis with certain length it is considered as a wave function like particle in one dimensional box (hypothetical situation).

5.Is ψ =e^iax  a wave function?

Mathematically it represents a wave. But it is not square integrable. So, it can not represent any physical system.

Read More:-