Acceleration

Acceleration is defined as the rate of change of velocity of a body. It is a vector quantity and it defines how quickly a body changes its velocity. If we set a speed limit for two bodies, the body which has more acceleration attains the targeted speed first and covers a set distance quickly. It is a derived quantity. Acceleration occurs when a body increases its speed, decreases its speed, or changes its direction.

Symbol	\vec{a},a
S.I. Unit	m/s2
Dimension	LT-2
Vector/Scalar	Vector
Fundamental/Derived	Derived

Though the unit of acceleration can be km/s², ft/s², mi/s² but in practice we use m/s² (S.I unit).
When a car increases its velocity, we are pushed back and when break is applied, we are pushed ahead. Similarly, when we take a sharp turn, we experience a force in the opposite direction.In all of these cases, we experience acceleration.

Derivation of acceleration:-

Newton’s second law of motion says that the rate of change of momentum is directly proportional to the applied force and takes place in the direction of the force.

F=\frac{\Delta p}{\Delta t}
\Rightarrow F=m\frac{\Delta v}{\Delta t}
\Rightarrow F=ma

Now, we can say that acceleration is directly proportional to the force and inversely proportional to the mass. But the force should be unbalanced. Because balanced force creates zero acceleration.

Sign conventions of acceleration:-

If we assign a particular direction ” X ” with positive sign and ” X’ “with negative sign then the corresponding positions are described with +ve i.e. (+1,+2,+3 etc.) and -ve signs. i.e (-1,-2,-3 etc.). respectively.

1. Fig. A – The car is moving with increasing velocity from A to B. Here its acceleration will be taken as positive (+) as it is working in the positive direction (X) of the predetermined co-ordinate system.

2. Fig. B – The car is moving with decreasing velocity from A to B. Here its acceleration will be taken as negative (-) as it is working in the negative direction (X’) of the predetermined co-ordinate system .

3. Fig. C – The car is moving with increasing velocity from A’ to B’. Here its acceleration will be taken as negative (-) as it is working in the negative direction (X’) of the predetermined co-ordinate system .

4. Fig. D – The car is moving with decreasing velocity from A’ to B’. Here its acceleration will be taken as positive (+) as it is working in the positive direction (X) of the predetermined co-ordinate system.           

How to calculate the acceleration :-

Consider a body moves towards the east from A to B. While moving it changes its velocity from 5 m/s to 15 m/s in 5 sec.

Then its acceleration = \frac{15-5\frac{m}{s}}{5s}=2\frac{m}{ s^{2} }

If we inverse the situation i.e.  the body decreases its velocity from 15 m/s to 5m/s in 5sec.

Then, its acceleration = \frac{5-15\frac{m}{s}}{5s}= - 2\frac{m} { s^{2} }

Here the -ve sign means decreases in velocity or acceleration in the opposite direction. The decrease in velocity is called deceleration.

Acceleration, velocity and displacement: –

Acceleration is the ratio of change in velocity to the time duration. Again, velocity is the time derivative displacement. So, acceleration is the second order derivative of displacement.

a=\frac{\mathrm{d} v}{\mathrm{d} t}
\Rightarrow a=\frac{\mathrm{d}}{\mathrm{d} t}( \frac{\mathrm{d} s}{\mathrm{d} t})
\Rightarrow a=\frac{\mathrm{d^{2}}s }{\mathrm{d} t^{2}}

Different types of acceleration:-

Average acceleration: –

Average acceleration is defined as the ratio of net change in velocity to the net time duration.
Average acceleration= \frac{V_{f}-V_{i}} { t_{f}-t_{i}}=\frac{\Delta V}{\Delta t}

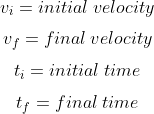
If a body started with velocity of 2m/s and attains a velocity of 6m/s in a duration of 2sec then its acceleration = \frac{6-2\frac{m}{s}}{2s}= 2\frac{m} { s^{2} }

Instantaneous acceleration:-

Instantaneous acceleration of a body is defined as the acceleration at a particular time.
Instantaneous acceleration is the average acceleration in a very very small time interval \Delta t\rightarrow 0

Uniform/constant acceleration:-

In physics both the concepts of uniform acceleration and constant acceleration are similar. When a body changes equal velocity in each equal interval of time, the acceleration is caused called uniform acceleration. A uniformly accelerated body moves with (possess) constant acceleration.

Graphical representation:-

1.velocity ~ time graph:-

The velocity ~ time graph of uniformly accelerated body is a straight line inclined to time axis. The body covers unequal distance in equal interval of time. The slope of the line give acceleration of the body.

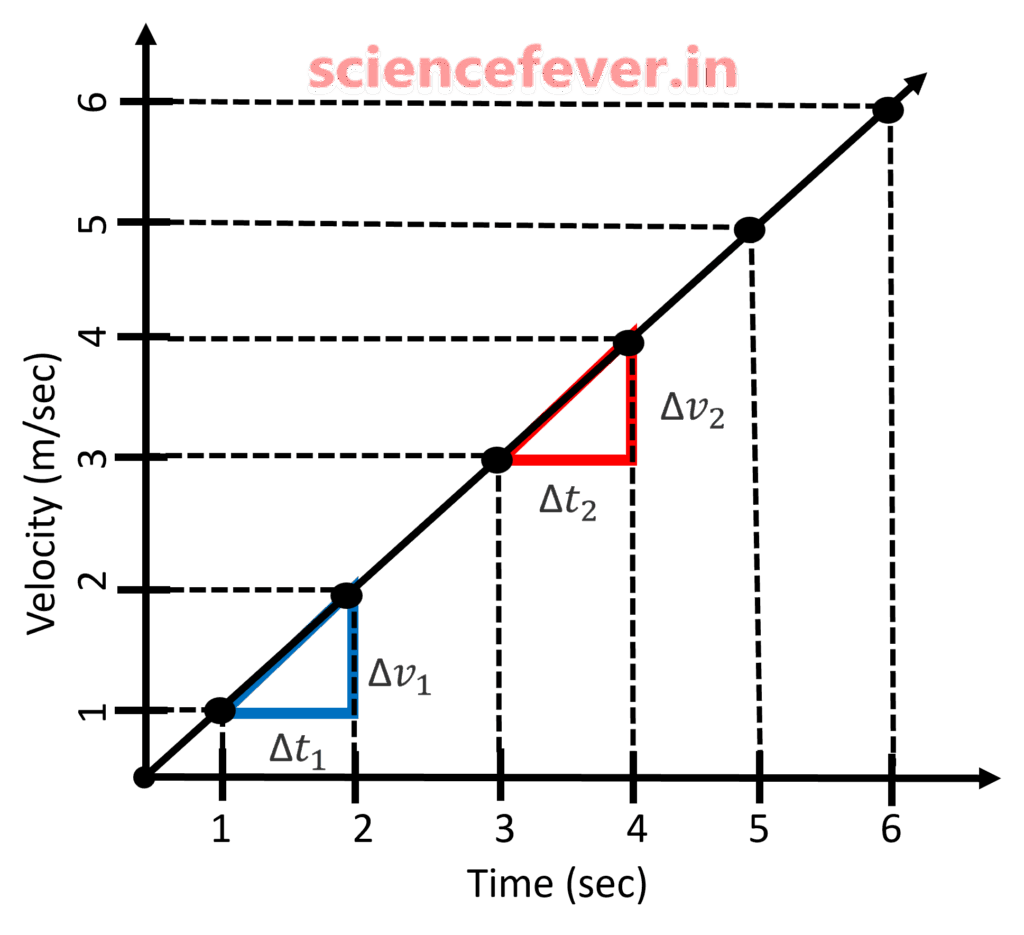
From the figure 2 it is noticed that;

\frac{\Delta v_{1}}{\Delta t_{1}}= \frac{\Delta v_{2}}{\Delta t_{2}}
\Rightarrow a_{1}=a_{2}

2. acceleration ~ time graph:-

Since the slopes of the v ~ t graph (acceleration) of an uniformly accelerated body always give equal values , so the a ~ t graph will be;

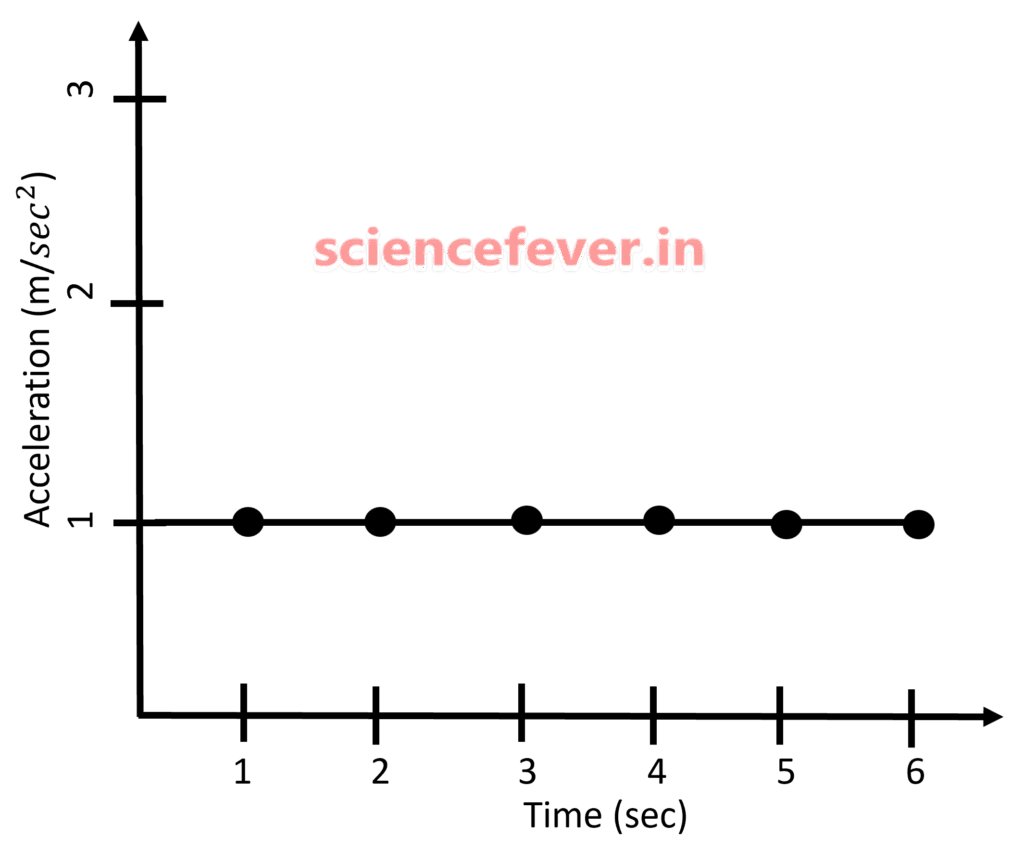
So, when a problem a mentions “A uniformly accelerated body with an acceleration of “a” m/s²” you have to put that value in the kinematic equations to get the required results.
The best example of uniform acceleration would be the motion of a body only under the influence of gravity.

Acceleration due to gravity (g): –

The gravitational force of earth attracts everything towards its center. This force causes an acceleration of 9.8 m/s² towards its center known as acceleration due to gravity.

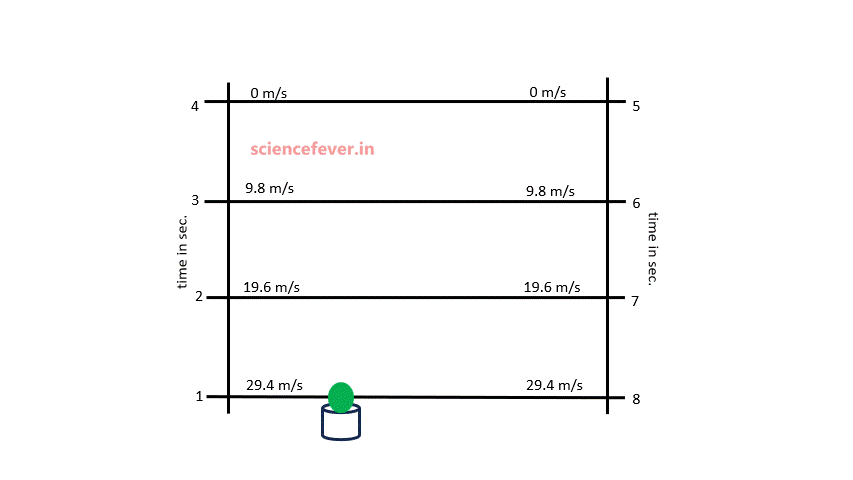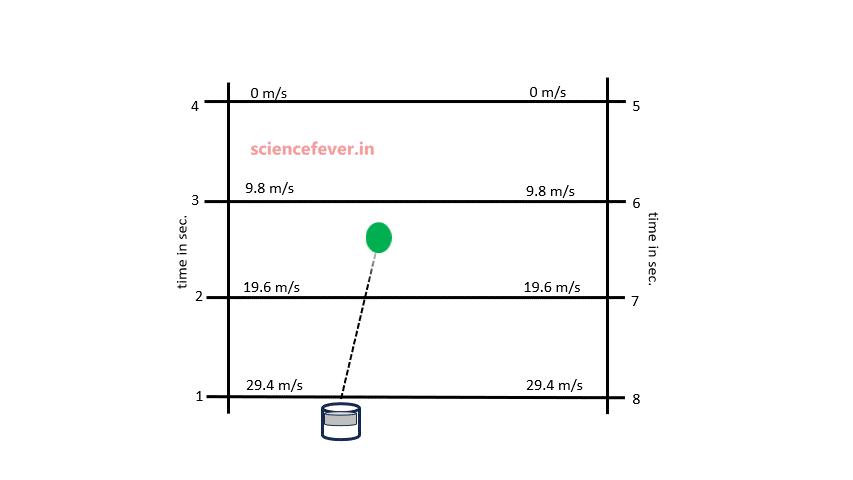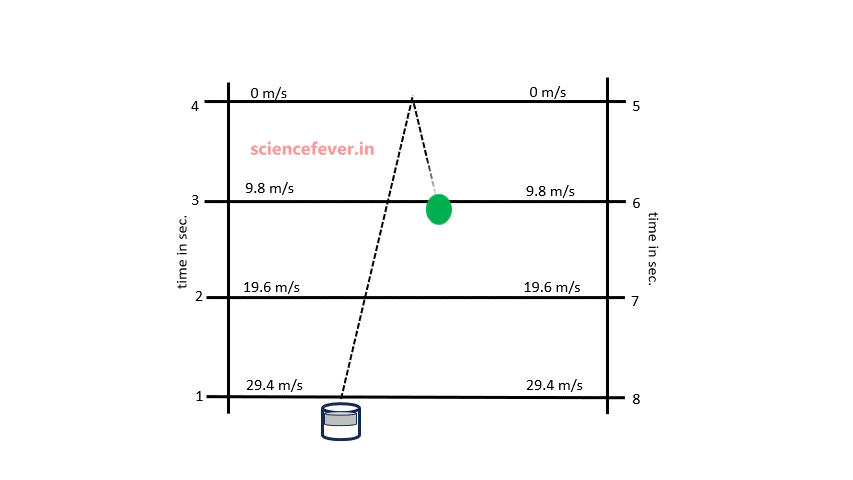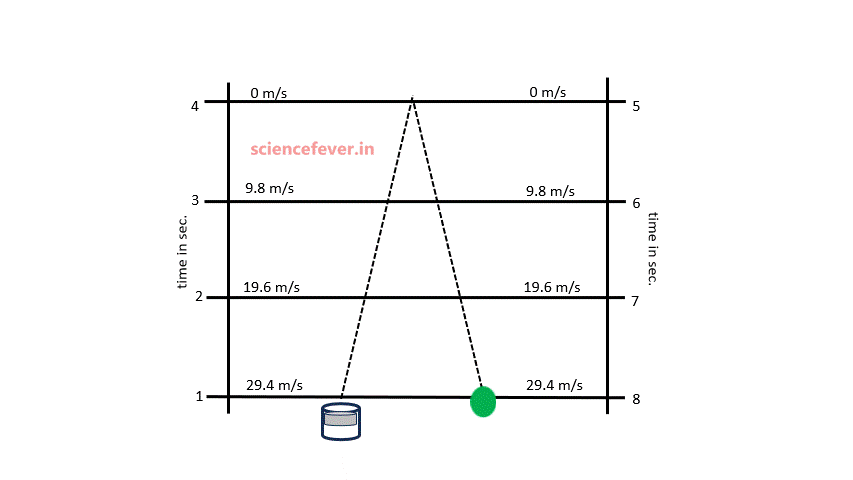
Consider a body thrown with an initial velocity of 29.4 m/s. As the acceleration due to gravity is 9.8m/s², the velocity of the body changes at 9.8m/s per sec. When the body moves upward its velocity decreases and when it moves downward its velocity increases. The velocities at different instants are shown in the animation.

Non-uniform acceleration: –

If the velocity delta is unequal for every equal interval of time, the acceleration is called non-uniform acceleration.

Circular motion:-

i.Angular acceleration: –

Suppose a body moves in a circular path, then its angular velocity
\omega =\frac{\Delta \Theta }{\Delta t}
Its angular acceleration   \alpha =\frac{\Delta \omega }{\Delta t}
Its direction will be along the axis of rotation.

ii.Centripetal acceleration: –

When the body moves in circular path the ‘centripetal force ‘acts upon it to keep its motion in the circular path. The centripetal force (towards center) creates centripetal acceleration (towards the center ) which is perpendicular to its direction of motion.
a=\frac{V^{2}}{r}

Problems: –

Q1.When a body started its motion with an initial velocity of 0 m/s and reaches 15m/s in 3sec. Then calculate the acceleration of the body.
Answer-
u=0\ m/s
v=15\ m/s
a=\frac{15-0}{3}= 5 m/s with direction.

Q2.If the velocity of a body is given the equation V (t)= t² + t , then calculate the acceleration of the body at 3 sec.
Answer–   
V(t) = t^{2} + t
\Rightarrow a=\frac{\text{d}V}{\text{d}t}\mid _{t=3}=2t+1=2*3+1=7\ m/s^{2}